1. 引言
- 所谓编译,就是高级语言转换为目标程序代码的过程
- 分为五部分
- 词法分析:分析源程序构成的字符串,转化为一个个的单词,留待下一步分析
- 语法分析:根据语言语法规则,把单词合成语法单位,如句子等
- 语义分析及IR的生成:根据第二步的语法分析,将其翻译成中间代码
- 中间代码一般含义明确
- 代码优化:这一步的任务是对第三步的中间代码进行等价变换,节省时间空间
- 目标代码生成:中间代码变成特定机器上的机器代码
2. 形式语言理论基础
形式语言基本概念
形式语言,顾名思义,我们只关心语言的“形式”,不关心具体含义
- 形式语言是一种不考虑含义的符号语言
- 形式语言主要研究:如何用严谨的数学规则来定义、产生和识别字符串的集合
符号:语言中最小的不可再分的基本单位
符号串:符号的有序序列,空字符串记作ε (ε不是空格)
字母表:非空的有限集合,集合里是符号即字母表的元素
符号串集合:代表了利用字母表能拼凑出的所有可能的字符串
我们给出语言/形式语言的具体定义:
语言/形式语言:字母表上所有符号串组成的集合的子集,用L表示。
- 语言是符号串集合的任意一个子集
符号串运算
- 符号串相等:必须所有符号依次相等
- 字符串长度:符号串中包含字符的长度
- 符号串连接:ab*bc = abbc
- 符号串的逆:倒置,abc -1 = cba ε-1 = ε
- 符号串的前缀,后缀,字串:以abc举例
- 前缀:ε a ab abc
- 后缀:ε c bc abc
- 子串:ε a b c ab bc abc
- 符号串集合的乘积:A={ab,bc},B={bc,b}
- AB={abbc,abb,babc,bab}
- {ε}A=A{ε}=A
- 符号串的幂:ω0=ε;ω1=ω;ω2=ωω;……;ωn=ωn-1ω
- ω=ab
- ω0=ε
- ω1=ab
- ωn=abab……ab
- ω1=ab
- ω0=ε
- ω=ab
- 符号串集合的幂:A0={ε};A1=A;……;An=An-1A=AAn-1 (n>0)
- 例:A={ab, c}
- A0={ε},A1={ab, c},A2={abc, cab, abab, cc}
- 集合A的闭包和正闭包:
- 闭包 (Closure) 指的是通过某种运算,将一个集合扩展到“包含所有可能结果”的完整状态。
- 星闭包 A* =A0 ∪ A1 ∪ …… A+=AA*=A*A
- 正闭包 A+=A1 ∪ A2 ∪ …… A*= A0 ∪ A+
- 正闭包不包含空串
文法和语言的形式定义
再给一遍定义:
语言:所有句子组成的集合,有限集:枚举,无限集:文法
句子:抽象看成某个有限字符表上的字符串。
文法:形式上描述和规定语言结构的方法,用有限的手段描述无限的句子集合的方法之一
- 文法是一个四元组:
- G=(VN,VT,S,P)记为G[S]。V是字汇表,V= VT∪VN,S∈VN,VT∩VN=Φ
- Vt:终结符号集,字母,最终成果,不可以被分解替换
- Vn:非终结符号集合,中间变量,用来推到最终句子
- S:开始符号:推导起点,通过S一步步变换成最终的集合
- P:产生式/规则集合:形式是U ::= X 代表U可以被改写成X
- 文法是一个四元组:
巴斯克范式:
BNF文法(Backus-Naur Form),用来描述编程语言语法的一种数学表示法
<digit> ::= "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" <integer> ::= <digit> | <digit> <integer>第一行定义数字可以是0到9的任意一个
<符号>::=<表达式><符号>(非终结符):表示可以继续分解的概念(如“数字”、“运算符”)。::=:意思是“定义为”或“由…组成”。<表达式>:包含终结符(直接出现的字符)和其他非终结符。|:表示“或”,即多种可能的选择。
句型:文法G[S],G=(VN,VT,S,P)
- 由S推出的符号串X∈(VT∪VN)*称为句型。
- 推导 规约 | 箭头表示 箭头下加三角代表规约
- A->a 是一个规则,p1=bAb p2=bab 所以p1直接推导出p2 p2直接规约到p1
- 如果经过序列推导,那么就称为推导/规约,箭头上带个加号

- 如果a可以推导b 或者a=b 那么称为a广义推导b,

- 规范推导:每次替换最后边非终结符的直接推导
语言
- 文法G 产生的语言L(G)
- 空语言:由文法开始符号推不出任何句子
- 给定一个文法,就能从结构上唯一确定其语言,给定语言可以推出文法 但不唯一
- 文法G 产生的语言L(G)
语法树和二义性

- 子树
- 简单子树:只有两层的树
- 简单短语:简单子树的叶子节点
二义性:一个句子有两个不同的语法树
- 若文法所定义的某个句子,有两种不同的最左(or最右) 推导/规约,则具有二义性
- 最左/右推导/规约:每次选择最左/右的非终结符进行推导/规约
- 二义性导致语义不确定性,句子一样,但是可以有两种语法解释
- 解决
- 修改编译算法
- 修改文法,加入优先层等
- 不存在一种算法在有限步内判断二义性
- 在计算机科学中,我们无法写出一个通用的程序(算法),让它输入任意一个上下文无关文法(CFG),然后告诉我们这个文法“是”还是“不是”二义性的。
- 规则左部的符号在右部同时出现两次 or 两次以上,导致二义性
- 这里的“规则”指推导式(Production Rule)。如果一个非终结符(左部)在推导出的结果(右部)中出现了多次,且没有明确的优先级或结合律限制,就很容易产生二义性
- 先天二义性文法
- 如果一个上下文无关语言(CFL)的所有文法都是二义性的,那么这个语言就称为先天二义性语言,而生成该语言的文法即为先天二义性文法。
- 如果一个语言 L,没有任何非二义性的文法可以生成它,那么 L 就是先天二义性的。
有害规则 多余规则
A->A 二义性


如果一个文法没有有害/多余规则 那么这个文法称为压缩 化简过的
扩充文法:
类似头节点

这个是要确保每一个非终结符都要能够推出纯粹的终结符字符串
- 首先去遍历产生式,把所有推出来全终结符的非终结符收起来
- 然后递归,看谁能推出来上一步得到的集合U终结符集合构成的串。可以就加入 然后继续这一步骤
- 最后删除掉不在Vn中的非终结符(清理多余规则

这个要确保删掉那些从“开始符号”出发,无论如何也推导不到的符号和规则。
- 从S开始推 递推找到所有有用的非终结符
- 找完后 看哪些非终结符是没用的 直接删了

这一步是要简化推导过程,删掉一些没啥用的中间规则,消除这类规则的目的是为了减少推导步骤,使文法更加简洁高效。
- 依次对每一个非终结符A 构造一个集合 代表这个非终结符可以推到的非终结符
- 然后看这个集合,假如这个集合中有元素可以推到句子,就直接加上A-句子 这个规则

其目的是将文法中递推到空串的规则去掉,同时保证文法所定义的语言保持不变。
- 和2.2差不多 首先找能推出空串的非终结符号 化成集合,然后递归找相关的扩充
- 删去这些空规则
- 然后在已有规则里找一下集合里的非终结符,全删掉
- 扩充新规则,假如之前是A - BC 但是C推出来空 那么就改成A - BC | C

在构建语法分析器(特别是自上而下的 LL 预测分析器)时,左递归会导致程序陷入死循环。为了解决这个问题,我们需要将左递归规则转换为等价的右递归规则。
- 这个例子很明显了,首先如果不递归 左边一定是a
- 那么我们先把a写好 再用一个A‘ 来完成后续的递归b
扩充BNF表示法

可以用于消除左递归
文法和语言的Chomsky分类
3型文法:正规文法,正则文法
- 限制最严,规则左侧只能是一个非终结符,右侧必须是一个终结符/终结符后跟一个非终结符(左线性或右线性)
- 对于每一个左(右)线性文法,都存在一个与某等价的右(左)线性文法
- 与词法有关的文法一般属于3型文法
2型文法:程序设计文法,上下文无关文法,下推自动机PDA
- 左侧只能有一个非终结符,右侧可以是终结符和非终结符的任意组合。
- 替换非终结符时不需要考虑前后字符
- 描述语法结构
- 可以描述栈,所以可以处理嵌套结构,构成下推自动机
1型文法:上下文相关文法
- 要求产生式右边字符串长度不小于左边,替换符号必须在特定上下文环境中进行
- 线性有界自动机LBA
0型文法:无限制文法,短语结构文法
- 没有任何限制,左侧只要包含一个非终结符即可。
- 递归可枚举语言
- 图灵机
0-3限制逐渐增加,描述语言能力逐渐减弱
- 1型号不允许A-e 但是2-3允许
四种语言可分别被四种自动机接收

3.自动机理论基础
有限自动机
自动机从识别语言出发,定义了语言。自动机是具有离散输入/出系统的一种数学模型
- 文法:是从产生语言的角度定义了语言。
- 自动机理论:是编译程序词法分析的理论基础。
首先定义自动机
- 状态转换图:定义在字母表上的有向图,满足三个初始条件:

可以用这个图识别句子:从开始状态到终止状态经过的边上的符号序列。
有限自动机FA

- 没有栈 没有寄存器,只存储当前状态
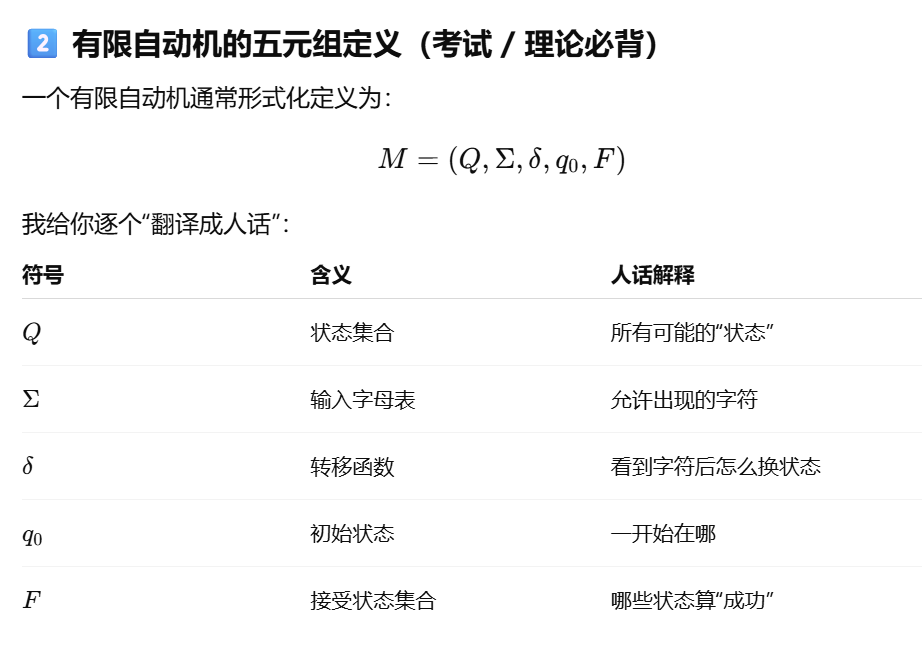
确定性有限自动机 DFA
非确定性有限自动机 NFA
写到这里 我决定面向押题学习了
————————————————————分割线——————————————————————
FIRST FOLLOW集
一、 FIRST 集的求法
FIRST 集的意义是:从非终结符开始推导,可能出现在字符串开头的第一个终结符的集合。

二、 FOLLOW 集的求法
FOLLOW 集的意义是:在某个句型中,紧跟在非终结符 A 后面可能出现的终结符的集合。






产生移进规约冲突 就不是LR0 直接SLR1 规约规约就看



LL1:
先优化文法,然后求first follow select 然后画表格 然后对输入串进行求解

DFA NFA
先优化表达式 然后画图,状态推导,最小化(小包大
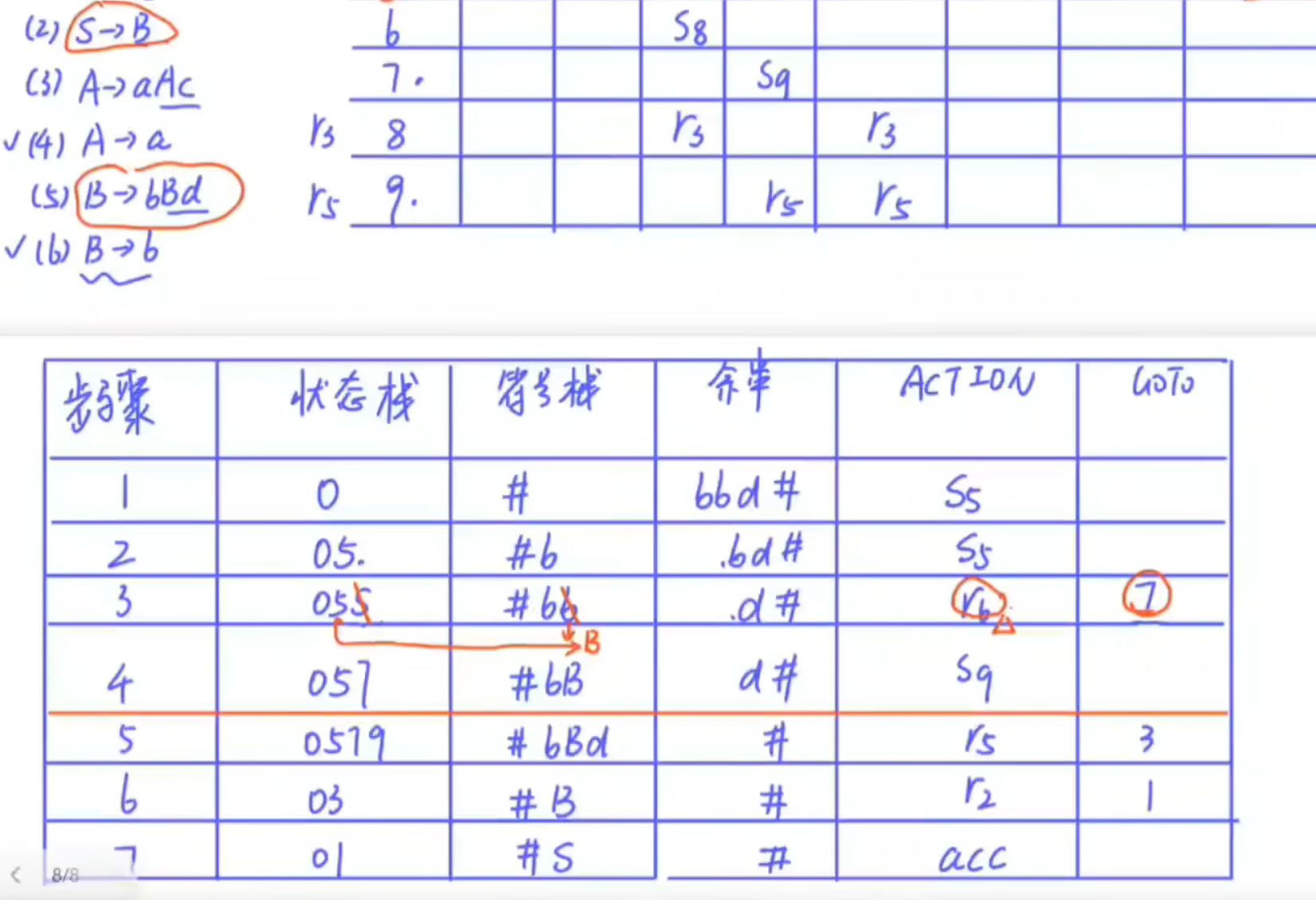
LR0 SLR1

SLR 先求follow集 再擦掉不在集里的r

LR1

LALR 合并同心

